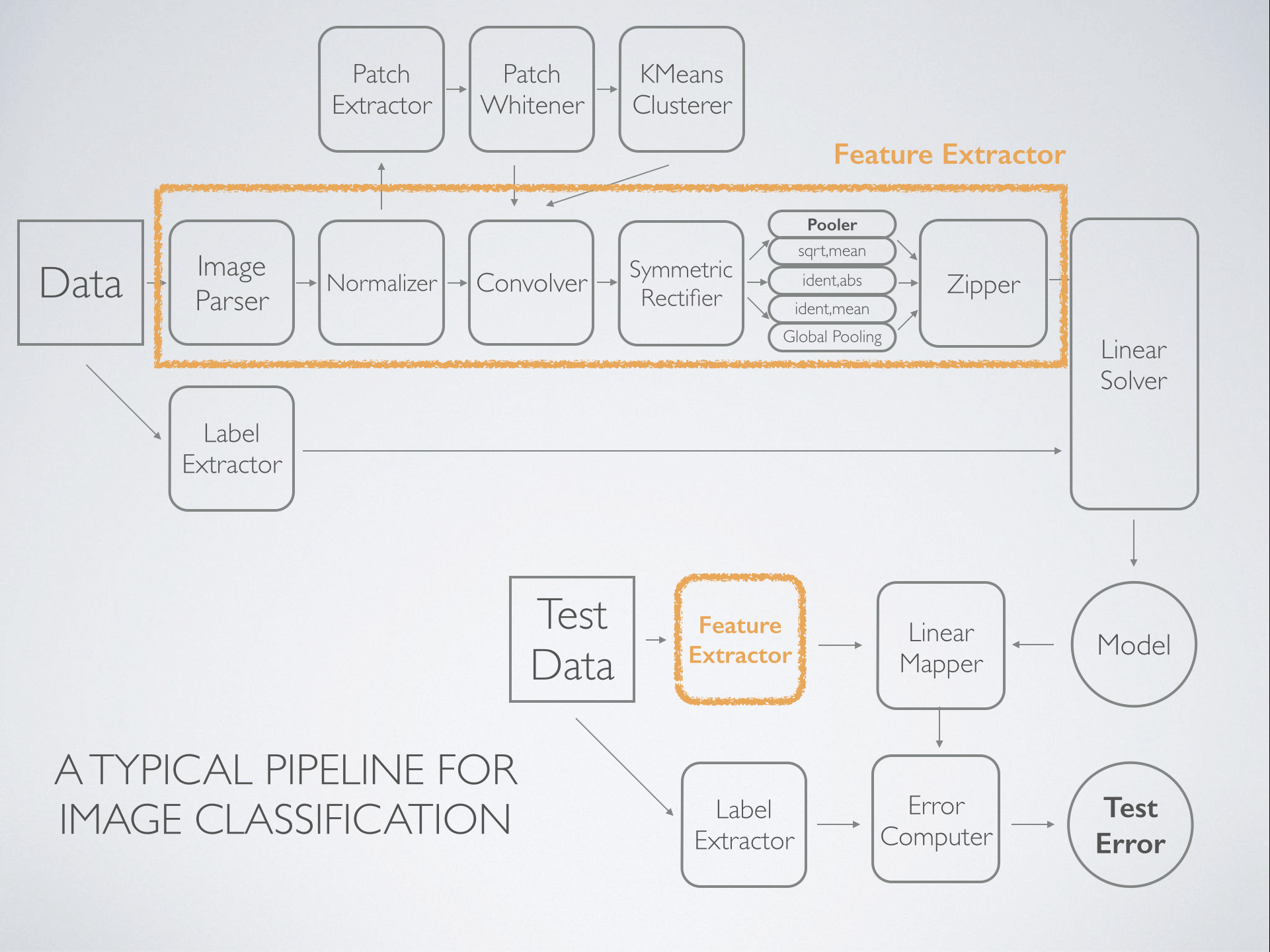
Classification
Statistical classification or discrimination is the problem of assigning categories to observations. If observations are drawn from distinct populations, and we would like to find a deterministic criterion that assigns the observations to their origin, the discriminant rule based on maximum likelihood would be $I(x) = \arg\max_{i \in K} f_i(x)$. Discriminant analysis are methods that provide estimators $\hat I(x)$ of such discriminant rules.
Notations: $K$, number of classes.
Algorithms
Linear discriminant analysis (LDA) assumes Gaussian populations with identical covariance matrices, which gives a linear discriminant rule [@Fisher1936]. Quadratic discriminant analysis (QDA) assumes Gaussian populations, giving quadratic discriminant rules. LDA and QDA are suitable for data with small $n$ or well separated classes, and are capable of $K>2$.
Naive Bayes suitable for data with large $p$
(kernel) support vector machine (SVM) SVM is computationally efficient on nonlinear kernels, suitable for data with well separated classes, but is limited to $K=2$.