Interval Estimation
Confidence Interval
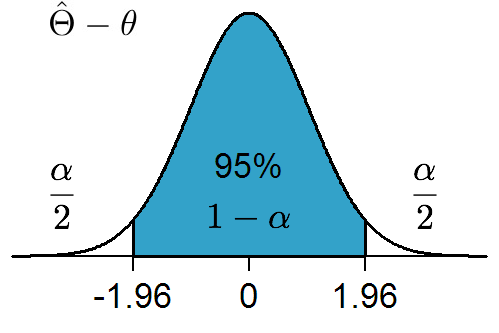 (Relative position of parameter.)
(Relative position of parameter.)
Given point estimators $\hat{\mathbf{\Theta}}$ of an unknown constant $\theta$, you may be able to construct a function of the estimators and the estimated that has a known probabilistic distribution. Confidence interval is a two-number summary of the support of this distribution with tails cut off.
In other words, confidence interval is a random entity determined by the tails of the distribution of a point estimator such that the unknown constant been estimated lies in the interval with some predetermined probability, typically 95%.
After a sample has been drawn, whether the unknown constant lies in the interval or not is not a matter of chance. But confidence interval shall be interpreted in the frequentist view that if repeated, 95 times out of 100 the computed intervals will include the unknown constant.
Confidence interval contains less information than the distribution of a point estimator.
Tolerance Interval
$X \sim F$ is an unknown quantity with continuous distribution. Find $a,b$, s.t. $P(X \in [a,b]) \leq 0.95$
Solution
Take random samples $X_1, \cdots, X_n$ , then $F(X_1), \cdots, F(X_n)$ i.i.d. $U[0,1]$ $$F(X_{(s)}) - F(X_{(r)}) \sim U_{(s)} - U_{(r)} \quad (s>r)$$ Let $P( F(X_{(s)}) - F(X_{(r)}) \leq 0.95 ) \geq 0.99$, which is equivalent to $$P( U_{(s)} - U_{(r)} \leq 0.95 ) \geq 0.99$$ Let $d = s-r$, and $\alpha = 0.95, \gamma = 0.99$, then $d$ satisfies $$F_{U_{(d)}} (\alpha) = \gamma$$ or $1-\alpha^d = \gamma$, so we get $$d = \frac{\log(1-\gamma)}{\log(\alpha)}$$