Interval Estimation

Confidence Interval

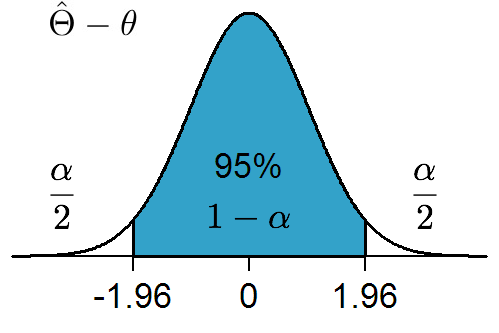(Relative position of parameter.)

Confidence interval is a random entity determined by its center and radius, both random variables, such that the unknown constant been estimated lies in the random interval with some predetermined probability, typically 0.95.

After a sample has been drawn, whether the unknown constant lies in the interval or not is not a matter of chance. But we can say that the constant lies in the interval with 0.95 confidence level.

"Confidence Distribution"

Information used to build a confidence interval is rich enough to derive a "confidence distribution" of parameter \( \theta \) relative to the confidence interval, more than simply a confidence level that \( \theta \) lies within it.

Tolerance Interval

\( X \sim F \) is an unknown quantity with continuous distribution. Find \( a,b \), s.t. \( P(X \in [a,b]) \leq 0.95 \)

Solution

Take random samples \( X_1, \cdots, X_n \) , then \( F(X_1), \cdots, F(X_n) \) i.i.d. \( U[0,1] \) \[ F(X_{(s)}) - F(X_{(r)}) \sim U_{(s)} - U_{(r)} \quad (s>r) \] Let \( P( F(X_{(s)}) - F(X_{(r)}) \leq 0.95 ) \geq 0.99 \), which is equivalent to \[ P( U_{(s)} - U_{(r)} \leq 0.95 ) \geq 0.99 \] Let \( d = s-r \), and \( \alpha = 0.95, \gamma = 0.99 \), then \( d \) satisfies \[ F_{U_{(d)}} (\alpha) = \gamma \] or \( 1-\alpha^d = \gamma \), so we get \[ d = \frac{\log(1-\gamma)}{\log(\alpha)} \]