Map Projections
A map projection is a coordinate transformation for points on the surface of a sphere or ellipsoid, typically in latitudes and longitudes (see Terrestrial Reference Systems). The projected coordinates are supposed to be plotted on a plane. All map projections distort the surface in some fashion, see map projection distortions visualized using d3. Because none is perfect for all needs, thousands of map projections are being used. Here is a nice comparison of map projections.
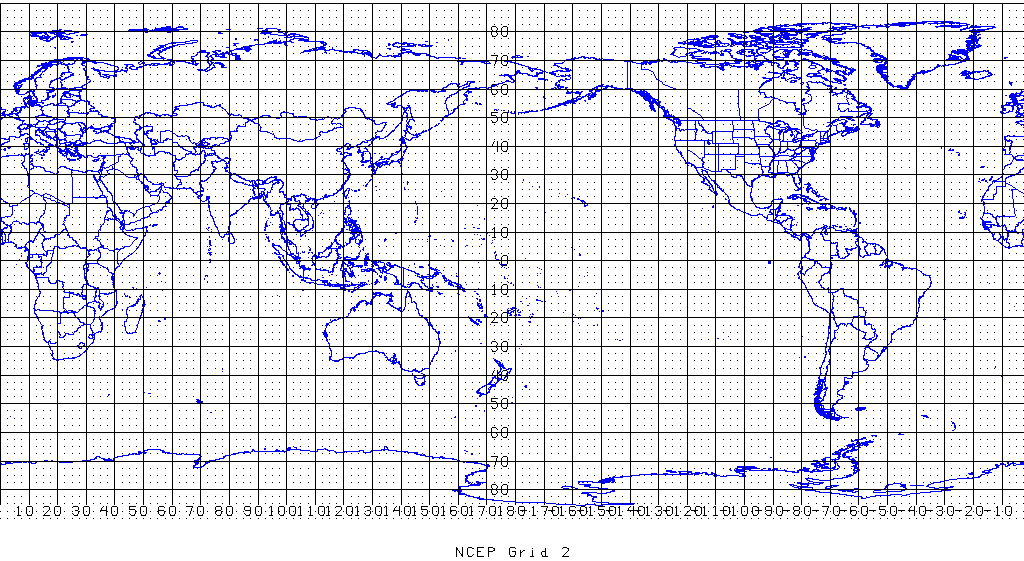
Mercator
Mercator projection is a cylindrical conformal projection: cylindrical mapping is north-up everywhere; conformal map (共形变换/保角变换) preserves the shape/angle of infinitesimal parts.
Mercator projection of a spheroid (ellipsoid of revolution) with semimajor axis a and eccentricity
(of meridional ellipse) e, given longitude λ and geodetic latitude φ:
$$x = a \lambda,\quad y = a \ln \left( \frac{1+\sin\varphi}{\cos\varphi} \cdot \left( \frac{1-e\sin\varphi}{1+e\sin\varphi}\right)^{e/2} \right)$$
Note that flattening f is related to eccentricity with: $e^2 = 2f - f^2$.
Mercator projection is standard for marine navigation, but is a notorious choice for world map, which theoretically has finite width but infinite height. Lengths away from the Equator are largely exaggerated, with (isotropic) local scaling factor:
$$k = h = \sqrt{1-e^2\sin^2\varphi} / \cos\varphi$$
PROJ.4 string for EPSG:3395 WGS 84 / World Mercator is:
+proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +datum=WGS84 +units=m +no_defs
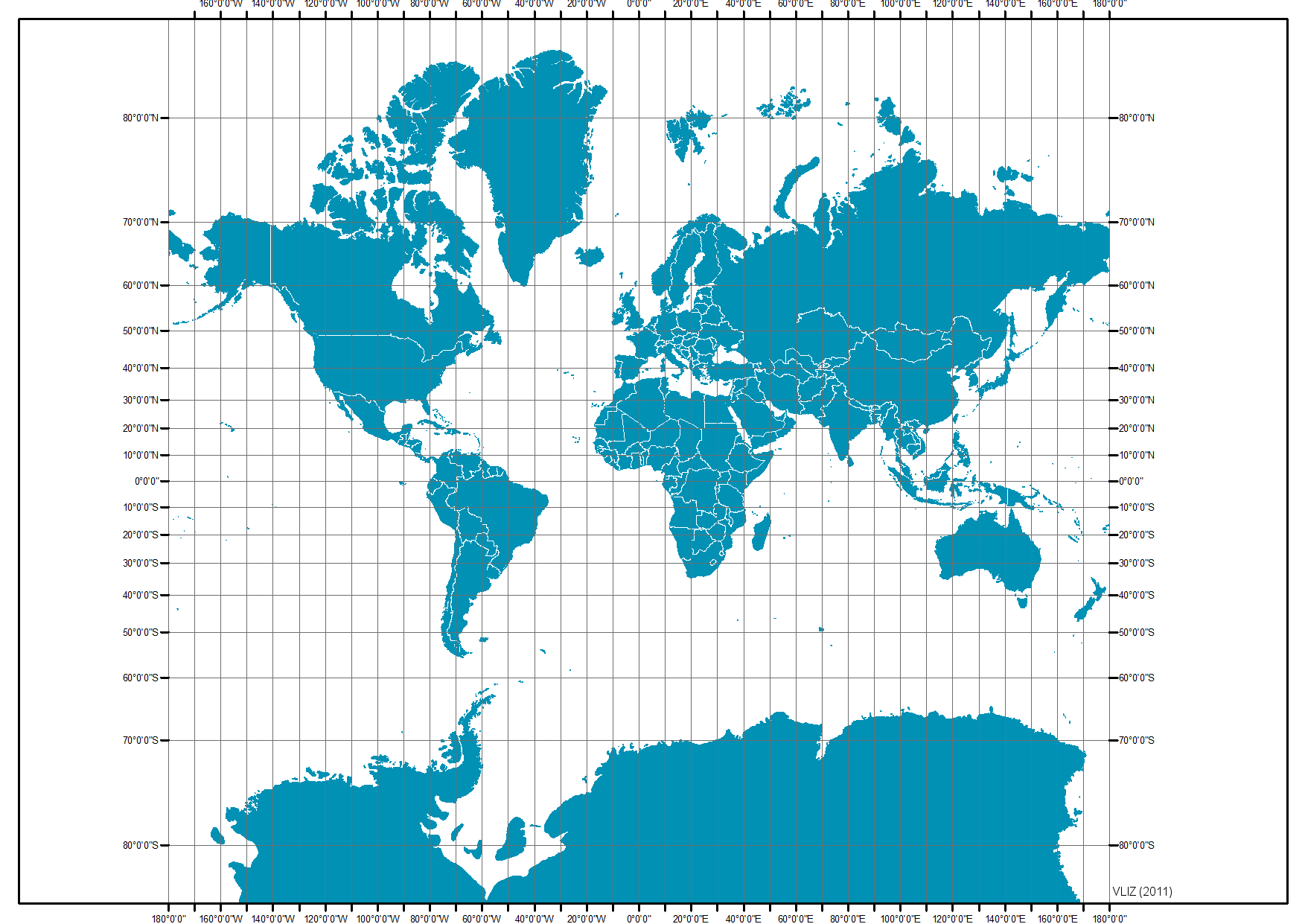
Web Mercator
Web Mercator, or WGS 84/Pseudo-Mercator (epsg:3857), is a variant of the Mercator projection
which projects WGS 84 longitude and latitude as if the flattening is zero,
thus not precisely conformal.
This projection was created by Google Maps and
is used by major online mapping services due to its computational simplicity.
Mercator projection of a sphere with radius r:
$$x = r \lambda,\quad y = r \ln \left( \frac{1+\sin\varphi}{\cos\varphi} \right)$$
Compared to WGS 84/ World Mercator (EPSG:3395),
WGS 84/ Pseudo Mercator (epsg:3857) has substantially larger $y$ coordinates increasing in latitude;
about 28km north at NYC (40.7° latitude).
If the flattening of WGS 84 was actually zero,
the local scaling factors will still be isotropic: $k = h = \cos\varphi$.
But Web Mercator is not strictly conformal, thus the above formula only serves as an approximation.
World maps projected in web Mercator are typically cut off at parallels near the poles
to make the resulting map square,
at latitude around ±85° ($\arctan(\sinh(\pi)) * 180/\pi \approx 85.05113$).
PROJ.4 string for epsg:3857 is:
+proj=merc +a=6378137 +b=6378137 +lat_ts=0.0 +lon_0=0.0 +x_0=0.0 +y_0=0 +k=1.0 +units=m +nadgrids=@null +wktext +no_defs
A null grid shift +nadgrids=@null prevents PROJ.4 from switching lng/lat coordinates
from spherical to WGS84; added in the PROJ.4 library since version 4.7.0.
Parameter +wktext preserves the exact PROJ.4 string in the WKT representation in GDAL/OGR.
Other Map Projections
Robinson
World. Pseudo-cylindrical. Compromise.
The earth is projected into track-and-field shape. Robinson is a great choice for a world map since it minimizes different kinds of distortion, although if you want to map individual countries or continents there are better choices in here tailored to specific parts of the world.
Winkel Tripel
World. Oval. Compromise.
A great choice for world maps. This compromise projection won't perfectly preserve areas, shapes, directions or distances, but it gets about as close as you can with a flat map. Good for wall maps and atlases.
Equirectangular (Plate carree)
World. Rectangular. Compromise.
If you're looking for a world map with a nice 'grid' appearance to the lines of latitude and longitude, this is a good choice, but be aware it doesn't preserve areas or shapes.
Cylindrical Equal Area
World. Rectangular. Size.
If you need a world map that is rectangular in shape and preserves areas (e.g., conformal), this is your only choice: Shapes are distorted (badly near the poles), but the relative sizes of places will be correct (good for dot density maps or choropleth).
Albers Equal Area Conic
Country. Size.
Good for world maps, but a great choice for making maps of the US, Canada, Europe, Australia and similarly-sized places: Areas are perfectly preserved and other distortions at this scale are minimal.