Mechanism Design
Play by the rules and beyond the rules.
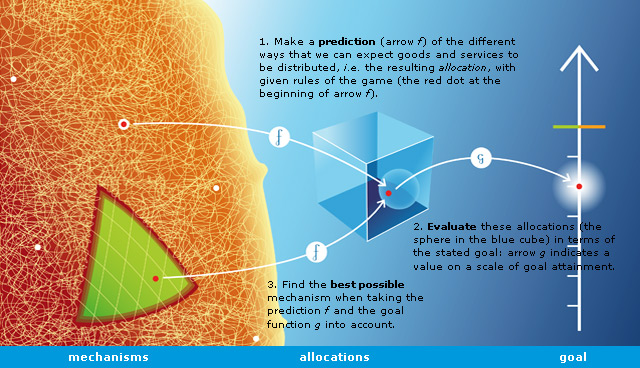
The power of game theory lies in changing rules of the game to make players play in an intended way. Mechanism design, aka reverse game theory, equates a mechanism with its equilibrium outcome and optimizes an objective over all feasible mechanisms.
Leonid Hurwicz, Eric Maskin and Roger Myerson are recognized 2007 Nobel Memorial Prize "for having laid the foundations of mechanism design theory". [@Hurwicz1960, 1972]
Concepts
Institution in political science, mechanism in economics, and game-form in game theory are synonymous: it defines the legal actions of each participant and the consequences of collective outcomes. A game-form is not a game, in that an outcome describes what happens, which need not have a mathematical formulation, while payoffs are how players are rewarded given the outcome. Mechanism design separates game-form from payoff functions and private information (e.g endowments and technologies): legislators have full control of the former but no control of the latter.
The true strategy space is the set of all feasible actions, which is a superset of the (legal) strategy space. Legal strategies are those prescribed by the mechanism governing the system; other feasible actions are illegal. The true game has the true strategy space and true outcome.
When you write the rules of the game you take into account that the players will try to cheat. [Hurwicz]
A mechanism can be seen as a communication system, where participants send messages to each other or to a “message center”, and a pre-specified rule assigns an outcome to each collection of received messages. [@Hurwicz1960] Mathematically, a mechanism is a function from the (legal) strategy/message space to the outcomes: $g: M \to Y$.
Each player has preferences over the outcomes, which may be formalized as utility function: $u_i: Y \times \Theta_i \to \mathbb{R}$, where parameter $\theta_i \in \Theta_i$ is referred to as the player's "type". Preference profile represents the collection of individual preferences: $\boldsymbol{\theta} = (\theta_i)_{i \in N}$.
Social choice rule (SCR) prescribes an appropriate outcome for each preference profile. Formally, it is a correspondence between preference profile space and outcome space: $f \subseteq \Theta \times Y$.
Implementation is an essential part of an institution, which means to have the money and the information to run the institutions, and there is legislation authorizing this. Enforcement of an institution is successful if the outcomes of the true game ensure that illegal strategies are (weakly) dominated by legal strategies. More broadly, implementation of an institution is successful if the equilibrium outcomes of the true game correspond to those envisioned by the legislation. (Nash equilibrium is neither self-enforcing nor self-implementing.)
Solution concepts in implementation: (in increasing order of sophistication)
- dominant strategy;
- Nash equilibrium in games of complete information;
- Bayesian Nash equilibrium in games of incomplete information [@Postlewaite1986];
Let $S(g, \boldsymbol\theta)$ be the set of equilibrium outcomes
A mechanism implements a social choice rule in a solution concept, if $S(g, \boldsymbol\theta) = f(\boldsymbol\theta), \forall \boldsymbol\theta \in \Theta$.
In that case, we say f is implementable in S. Nash equilibrium if the Nash equilibrium coincide with social optimum under all states: $f(\theta) = \text{NE}_g(\theta), \forall \theta$.
Constraints:
- Resource constraint: budget constraint (BC);
- A process is incentive-compatible (IC) if all of the participants fare best when they truthfully reveal any private information asked for by the mechanism [@Hurwicz1972];
- Participation constraint (PC): players must be at least as well off as if they had abstained;
Optimality criteria (of an outcome):
- (ex-post) Pareto efficiency: $\nexists y' \in Y: \mathbf{u}(y', \boldsymbol\theta) - \mathbf{u}(y, \boldsymbol\theta) \in \mathbb{R}_{\ge0}^N \setminus {0}$;
- A direct mechanism is said to be incentive efficient if it maximizes some weighted sum of the agents’ expected payoffs subject to their IC constraints.
A social choice rule is efficient if its outcome is efficient for each preference profile. A mechanism is efficient if its equilibria...
Pareto efficiency is incompatible with voluntary participation: For bilateral trade, no incentive compatible direct mechanism which satisfies (interim) participation constraints has the property that trade occurs if and only if there are gains from trade. [@Laffont1979, @Myerson1983]
In a standard exchange economy, no incentive-compatible (IC) mechanism with participation constraint (PC) can produce Pareto-optimal outcomes. In other words, private information precludes full efficiency.
Informationally decentralized [@Hurwicz1972]
General Theory
Revelation Principle
The set of all possible mechanisms cannot be represented parametrically, thus hard to study. Luckily, the revelation principle guarantees that truth-telling is an equilibrium.
Principal-agent (委托-代理) problem is a class of games with information asymmetry where one player (the principal) attempts to offer incentives to the other (the agent) to encourage the agent to act in the principal's best interest.
Information asymmetry [@Arrow1963; @Akerlof1970] can take the form of either hidden information (incomplete information) or hidden action (imperfect information). Complete information: all agents except the government could observe the preference profile. Incomplete information: each agent could observe only its own preference. Complete information applies when the agents all know one another well, but the authority is a comparative outsider. As of hidden information, adverse selection refers to the situation when the type of product is hidden from one party in a transaction. As of hidden action, moral hazard refers to the situation when individuals take greater risks when the cost is shared with other parties than taken alone.
Revelation principle: [@Gibbard1973; @Dasgupta1979; @Myerson1979, 1982, 1983, 1984] Any equilibrium of an arbitrary mechanism can be replicated by an incentive-compatible direct mechanism. Thus, when searching for the best possible mechanism to solve a given problem, it suffices to look within incentive-compatible direct mechanisms, a subclass of mechanisms that permits mathematical analysis. Once the best direct mechanism has been found, the researcher can “translate back” that mechanism into a more realistic mechanism.
Original mechanism: $h(m_1, \dots, m_n)$; Equilibrium: $\{s_i^∗ (t_i)\}_{i=1}^n$; Direct mechanism: $h^∗ = h \circ \mathbf{s}^∗$;
Implementation Theory
It is desirable to design mechanisms in which all equilibria are optimal for the given goal function.
Without stability under reasonable adjustment dynamics, the more sophisticated a game theoretic solution concept is, the less likely its prediction will be observed.
In quite general environments, the only dominant-strategy mechanism is dictatorship, whereby one pre-selected agent always gets his favorite alternative.
A social choice rule is monotonic if a social optimum in one state remains optimum in another as long as it does not decrease in any player's preference: $\forall \theta \in \Theta, a \in f(\theta)$, if $u_i(a, \theta) \ge u_i(b, \theta) \Rightarrow u_i(a, \theta') \ge u_i(b, \theta')$, $\forall i \in N, b \in A$, then $a \in f(\theta')$.
Nash implementation theorem: [@Maskin1977]
- If a social choice rule is implementable, it must be monotonic.
- A social choice rule is implementable if it is monotonic, no individual has veto power, and there are more than two players.
The plurality rule is not Maskin monotonic and thus cannot be Nash-implemented, as long as there are at least three alternatives.
No single-valued social choice rule can be Maskin monotonic. [@Muller1977]
A recent review of implementation theory. [@Serrano2004]
Specialized Theory
Characterizing the optimal institution for any given set of conditions. (public goods, auctions, contracts)
A theory of which market institutions will emerge. [@Myerson1981; Maskin and Riley 1984]
Efficient mechanism; Optimal mechanism
Market
The perfectly competitive market is the only efficient mechanism if there are: large numbers of buyers and sellers so that no single agent has significant market power; and no significant externalities, that is, an agent's consumption, production, and information does not affect others' production or consumption. [Maskin 2007 Nobel Price Lecture; @Hammond1979; @Jordan1982] However, mechanisms improving the market are generally possible if either assumption is violated. [@Laffont1985]
The greed process [@Hurwicz1960] has the desired optimality properties for all environments from which so-called external economies or diseconomies are absent; but it lacks the stability properties known to hold for perfect competition at least in certain special cases.
Auction
Auction is typically the most efficient institution for the allocation of private goods among a given set of potential buyers.
- Double auction (buyers and sellers both post their prices);
- Second-price auction (Vickrey auction);
Double auction is mathematically equivalent to the direct mechanism in which each party announces its valuation and the object changes hands at a price between the announced valuations if and only if the owner’s value is lower than the buyer’s.
A general revenue-equivalence theorem: [@Myerson1981] English, Dutch, first-price sealed bid, and second-price sealed bid auctions generate the same expected revenue. If the bidders are "symmetric" and if the seller sets an appropriate reserve price, then all of the four auction formats are incentive efficient.
Double auctions are incentive efficient. [@Wilson1985]
Public Goods
Samuelson's conjectures: [@Samuelson1954; @Hurwicz1972]
- Truthful revelation of preferences is not a Nash equilibrium in the Lindahl game.
- There may be no successful implementation for public goods under decentralization.
There is often no good market solution to the problem of providing public goods. The efficient provision of public goods may require substantial departures from the principles of unanimous decision-making.
Dominant-strategy mechanisms for public goods provision: Vickrey-Clarke-Groves mechanism [@Vickrey1961; @Clarke1971; @Groves1973] If there are no income effects (quasi-linear utility function) on the demand for public goods, then there exists a class of mechanisms in which: (a) truthful revelation of one’s willingness to pay is a dominant strategy, and (b) the equilibrium level of the public good maximizes the social surplus. However, the mechanism does not in general satisfy budget balance [@Green1979].
Bayesian mechanisms for public goods provision: d’Aspremont’s and Gérard-Varet’s (1979) mechanism are fully Pareto efficient, but violates (interim) participation constraints.
The probability of funding a public goods project tends to zero as the number of agents increases, despite everyone knowing that they can be jointly better off if the project is funded. [@Mailath1990]
A proposed solution to the public goods problem using neural measures of economic value. [@Krajbich2009]
Others
Interdependent valuations. [@Jehiel2001]
Applications
(Applied) mechansim design is the engineering aspect of game theory / economics, complemented by experiments and computation. [@Roth1999]
Regulatory insitutions. [@Baron1989]
Railroad privatization. [@Brewer1996]
Electromagnetic spectrum. Online advertising.
Market Design
Market(place) design. (Alvin Roth [@Roth1999; @Roth2002]; Scott Kominers, student of Roth [@Kominers2018])
Marketplace consists of rules that govern which (and when) transactions occur, and infrastructure that aids market participants in choosing and completing transactions. Market design seeks to increase allocative efficiency, transaction liquidity, or equity/fairness in marketplaces, via:
- Rules innovations:
- market-clearing mechanism (re-)design [@Roth1999]: refugee resettlement [@Delacretaz2016];
- limiting permitted transactions [@Milgrom2010];
- Infrastructure innovations:
- information provision [@Athey2014]: entry-level labor market certification;
- simplifying or promoting entry [@Djankov2002]: college application;
- creating market(place) architecture and interfaces [@LiSW2017]: Chicago HealthLNK;
Algorithmic Mechanism Design
Algorithmic mechanism design. [@Nisan2001; @Nisan2007; @Nisan2015] Uncertainty in algorithms and mechanisms. Online markets. (Stefano Leonardi of Sapienza University of Rome)
mechanism representation complexity: menu size bounds. [@Daskalakis, Deckelbaum, Tzamos, 2014] computational complexity of finding the optimal mechanism: sample complexity (value prior from samples); communication complexity; strategic complexity (obviously strategy-proof); complexity in preference elicitation; [@Yannai A. Gonczarowski's dissertation, 2018]
Others
Transportation. Service procurement. [@SongJJ2003] Congestion pricing. [@WuD2012] Parking slot assignment. [@ZouB2015] On-demand transportation. [@Egan2016]
Supply chain management. Liner shipping carriers. [@Agarwal2010] Freight. (Maged Dessouky [@Furuhata2015; @ZhangWT2018; @ZouH2018, now Carlsson2018]) E-commerce logistics. [@XuSX2015]
Social mobilization. [@Pickard2011]
References
Monograph: [@Hurwicz2006] Surveys: [@Maskin1999; @Baliga2003]