Critical Point

Classification: linear case

For a linear 2nd-order ODE system, \[ \mathbf{y}' = B \mathbf{y} \]

If \( B \) has real eigenvalues \( \lambda, \mu \), e.g. \( B = \begin{pmatrix} \lambda & 0 \\ 0 & \mu \end{pmatrix} \) , then \( \begin{cases} y_1 = y_1(0) e^{\lambda t} \\ y_2 = y_2(0) e^{\mu t} \end{cases} \)

  1. Source: \( (\lambda > \mu > 0) \)
  2. Sink: \( (\lambda < \mu < 0) \)
  3. Saddle: \( (\lambda > 0 > \mu) \)

If \( B \) has two complex conjugate eigenvalues \( a \pm ib \), e.g. \( B = \begin{pmatrix} a & b \\ -b & a \end{pmatrix} \) , then \( \begin{cases} y_1 = A e^{at} \sin(bt+\phi) \\ y_2 = A e^{at} \cos(bt+\phi) \end{cases} \)

  1. Unstable focus (focus): \( (a > 0) \)
  2. Stable focus (foci): \( (a < 0) \)
  3. Center: \( (a = 0) \)

Note:

  1. Linear systems have one or a line of critical points, since \( B \text{y} =0 \) has a unique solution or a set of solutions with dimension 1.
  2. Closed orbits exist around a center, and have the same period, but nonlinear systems are not so.
  3. For a nonlinear system, a center found in its linearized form made not be an actual center; symmetry of the original system about \(y\)-axis suffice to preserve this property.

Procedure: nonlinear case

For a nonlinear 2nd-order ODE system: \[ \frac{\text{d}}{\text{d}t} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} f(x,y) \\ g(x,y) \end{pmatrix} \]

  1. Find critical points: \( \begin{pmatrix} f(x_0,y_0) \\ g(x_0,y_0) \end{pmatrix} = 0 \)
  2. Linearize at the critical points: \( \frac{\text{d}}{\text{d}t} \begin{pmatrix} x \\ y \end{pmatrix} = \nabla\begin{pmatrix} f(x,y) \\ g(x,y) \end{pmatrix}\bigg\rvert_{(x_0,y_0)} \begin{pmatrix} x-x_0 \\ y-y_0 \end{pmatrix} + \text{h.o.t.} \)
  3. Switch axes to the critical point and get \[ \frac{\text{d}}{\text{d}t} \begin{pmatrix} \tilde{x} \\ \tilde{y} \end{pmatrix} = A \begin{pmatrix} \tilde{x} \\ \tilde{y} \end{pmatrix} \] , where \(A\) is the Jacobian evaluated at the critical point.
  4. Normalize the coefficient matrix with \(P\), s.t. \( B= P^{-1}AP \) is a Jordan matrix.
  5. Solve the system w.r.t. \( P^{-1} \begin{pmatrix} \tilde{x} \\ \tilde{y} \end{pmatrix} \) as linearized cases.

Note:

  1. To get the phase plane of \(\begin{pmatrix} x \\ y \end{pmatrix}\) near the critical point, we just need to do a coordinate transformation, which doesn't change the type of critical point. Hence the eigenvalue of \(A\) determined the type of critical point.
  2. Eigenvector and orbit. If \(\begin{pmatrix} x_1 \\ y_1 \end{pmatrix}\) is an eigenvector of the linearized system, corresponding to eigenvalue \( \lambda \), along the line of the eigenvector we have \( \frac{\text{d}}{\text{d}t} \begin{pmatrix} x \\ y \end{pmatrix} = \lambda \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} \). This means in the direction of the eigenvectors from the critical point, the orbit goes directly away from or into the critical point, approximately in a straight line.

Plane Analysis of 2nd-order ODE Systems

Duffing equation

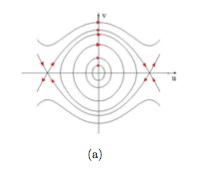Trajectories in the Duffing equationTrajectories in the Duffing equation

A form of Duffing equation is

\[ u'' + u - u^3 = 0 \]

Or, in the form of ODE systems,

\[ \begin{cases} u' = v \\ v' = -u+u^3 \end{cases} \]

We find three critical points: \( (0,0) \) and \( (\pm 1,0) \). Furthermore, the first one is a center, and the other two are saddles.

Heteroclinic & homoclinic orbit

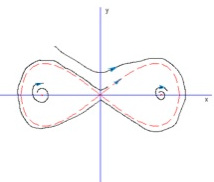Homoclinic orbitsHomoclinic orbits

A trajectory may connect two critical points, or forms a loop from and toward the same critical point. The former one is called a heteroclinic orbit, and the latter a homoclinic orbit.

We've already seen heteroclinic orbits in duffing equation, now we illustrate a homoclinic oribt by the following system.

\[ \begin{cases} x' = y + y(1-x^2)[y^2-x^2(1-\frac{x^2}{2})] \\ y' = x(1-x^2) - y[y^2-x^2(1-\frac{x^2}{2})] \end{cases} \]

There are also three critical points: \( (0,0) \) and \( (\pm 1,0) \). The origin is a saddle, while the other two are unstable focus (foci).

Note: Period of homoclinic or heteroclinic orbit

  • Generally, homoclinic and heteroclinic orbits go from and to saddle points. Since near saddle points, along the direction of eigenvectors, \( y'= \lambda y \), it takes infinite time to go to or leave the critical point.
  • Hence, homo- and hetero-clinic orbits are typically with infinite period.

Limit cycle

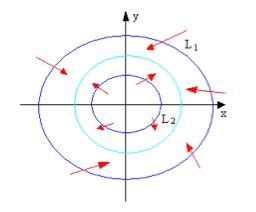The Poincare-Bendixon theorem and limit cycleThe Poincare-Bendixon theorem and limit cycle

A limit cycle is a closed orbit that each trajectory nearby either goes towards it, or leaves away. It is another important type of closed orbits.

Certain theorems guarantee the existence of a limit cycle.

Poincare-Bendixon Theorem:

  • Assume that \(B\) is a ring-shaped domain between two simple closed curves \(L_1\) and \(L_2\). There is no critical point in this domain. Moreover, any trajectory that intersects with these two curves enters \(B\). Then there exist at least one limit cycle in this domain.
  • The conclusion holds if the inner boundary curve \(L_2\) shrinks into an unstable node.

van der Pol equation

Stability and Lyapunov Function

Bifurcation Theory

Chaos

Notes yet to be digitized

References

  1. 王联、王慕秋, 非线性常微分方程定性分析. 哈工大出版社,1987.
  2. 黄永念，非线性动力学讲义，2004.
  3. J. Smoller, Shock Waves and Reaction Diffusion Equations, Springer (1994)
  4. P Grindrod, Patterns and Waves, Claredon, 1991
  5. G. B. Whitham, Linear and Nonlinear Waves, John Wiley & Sons (1974).

🏷 Category=Dynamical System