Stochastic Convergence
Stochastic convergence is the convergence of R.V. & Distributions.
Convergence concepts are build on topologies, which is commonly specified by a metric on a metric space.
Convergence of random variables
Convergence mode, notation, $(\mathcal{L}, d(\cdot,\cdot))$:
- Sure convergence ($e$): $(\mathbb{R}, |\cdot|)$, pointwise in sample space;
- Almost sure convergence ($a.e.$): $(\mathbb{R}, |\cdot|)$, except for a measure-zero set;
- Convergence in probability ($p$): $(\mathcal{L}_p, \mathbf{E}\frac{|\cdot|}{1+|\cdot|})$;
- $l_r$ convergence ($l_r$): $(\mathcal{L}_r, \|\cdot\|_r)$;
Almost sure convergence
A simple sufficient condition for almost sure convergence is: $\forall \varepsilon >0, \sum_{n=1}^{\infty} P{ |X_n-X| \geq \varepsilon } < \infty$
Proof:
$$\begin{align} & X_n \xrightarrow{a.e.} X \\ \iff & P{ \lim_{n \to \infty} X_n(\omega) \neq X(\omega) } =0 \\ \iff & \forall \varepsilon >0, P{ lim_{n \to \infty} \cup_{m\geq n} { |X_m-X| \geq \varepsilon } } =0 \\ \iff & \forall \varepsilon >0, lim_{n\to \infty} P{ \cup_{m\geq n} { |X_m-X| \geq \varepsilon } } =0 \\ \Longleftarrow & \forall \varepsilon >0, lim_{n\to \infty} \sum_{m\geq n} P{ |X_m-X| \geq \varepsilon } = 0 \\ \iff & \forall \varepsilon >0, \sum_{n=1}^{\infty} P{ |X_n-X| \geq \varepsilon } < \infty \end{align}$$
Convergence in probability
The typical definition of convergence in probability is: $\forall a>0, \forall \varepsilon>0, \exists N\in \mathbb{N}: \forall n>N, P{ |X_n-X| \geq a } < \varepsilon$.
An alternative definition is based on metric space $\mathcal{L}_p$, where $\mathcal{L}_p$ is the space of r.v.'s with finite norm $\mathbb{E}\tfrac{|\cdot|}{1+|\cdot|}$, and the metric is the one associated with the norm. $\mathcal{L}_p$ space is complete.
It can be shown using basic inequalities that the two definitions are equivalent.
Stochastic order notation
We denote $X_n = o_p(1)$ if the sequence of random variables $\{ X_n \}$ converges to 0 in probability. Symbolically, $X_n \overset{p}{\to} 0$.
We denote $X_n = O_p(1)$ if the sequence of random variables $\{ X_n \}$ is uniformly bounded in probability. Symbolically, $\forall \varepsilon >0, \exists M>0: \limsup_{n\to\infty} P \{ \lvert X_n \rvert > M \} \leq \varepsilon$
It can be proved that manipulating rules for order in probability notation is in direct parallel to other big-O notations. For example, $o_p(1) + o_p(1) = o_p(1), \quad o_p(1) + O_p(1) = O_p(1), \quad O_p(1) + O_p(1) = O_p(1) \\ o_p(1) o_p(1) = o_p(1), \quad o_p(1) O_p(1) = o_p(1), \quad O_p(1) O_p(1) = O_p(1)$
Convergence in $\mathcal{L}_r$
The $\mathcal{L}_r$-norm of r.v. is $||\cdot||_r = ( \mathbb{E}|\cdot|^r )^{\frac{1}{r}}$
The $\mathcal{L}_r$ space of r.v.'s is almost a metric space, where the metric $L_r$-norm satisfies nonnegativity, symmetry, and triangle inequality (Minkowski's inequality), but positivity is not satisfied.
If we treat equivalence classes $[X] = \{ Y \in \mathcal{L}_r \mid Y=X \text{ almost surely} \}$ as fundamental points in the $\mathcal{L}_r$ space, then the $\mathcal{L}_r$ space becomes a metric space.
It can be shown that $\mathcal{L}_r (\mathcal{U},\mathcal{F},P)$ is complete, and $\mathcal{L}_2 (\mathcal{U},\mathcal{F},P)$ is a Hilbert space.
Hierarchy of r.v. spaces: $\mathcal{L}_p \supsetneq \mathcal{L}_1 \supsetneq \mathcal{L}_2 \supsetneq \cdots \supsetneq \mathcal{L}_{\infty}$
Convergence of distribution functions
Convergence of distribution functions is pointwise convergence to some distribution function, except for its discontinuous points. The underlying metric space is $([0,1],|\cdot|)$. Denoted as $\mathbf{X}_n \Rightarrow \mathbf{X}$.
The corresponding sequance of random variables is said to converge weakly.
Note:
- It's possible for a sequence of distribution functions to converge pointwise to a function that is not a distribution function.
- Other definitions are weak convergence and convergence is Levy metric. The three definitions can be shown to be identical.
- The (perhaps) only general theorem on asymptotic distribution is the CLTs, which is based on sample average, or at least the average of a series of random variables. Other types of sequences of r.v.'s do not have an easy result for their limiting distribution.
Cramér–Wold theorem
A series of random vectors converges in distribution iff all its one-dimensional projection also converges in distribution.
Weak convergence of probability measures
Definition: (the portmanteau theorem) Let S be a metric space with its Borel σ-algebra Σ. We say that a sequence of probability measures ${ P_n }$ on (S, Σ) converges weakly to the probability measure P, if and only if any of the following equivalent conditions is true:
- $\mathbb{E}_n f \Rightarrow \mathbb{E} f$ for all bounded, continuous functions f;
- $\mathbb{E}_n f \Rightarrow \mathbb{E} f$ for all bounded and Lipschitz functions f;
- $\limsup \mathbb{E}_n f \leq \mathbb{E} f$ for every upper semi-continuous function f bounded from above;
- $\liminf \mathbb{E}_n f \geq \mathbb{E} f$ for every lower semi-continuous function f bounded from below;
- $\limsup P_n (C) \leq P(C)$ for all closed sets C of space S;
- $\liminf P_n (U) \geq P(U)$ for all open sets U of space S;
- $\lim P_n (A) = P(A)$ for all continuity sets A of measure P.
In the common case when $S=\mathbb{R}$ with its usual topology, then weak convergence of probability measures is equivalent to convergence of distribution functions.
Weak convergence of probability measures is denoted as $P_n \rightarrow P$.
Properties
Relations of convergence modes
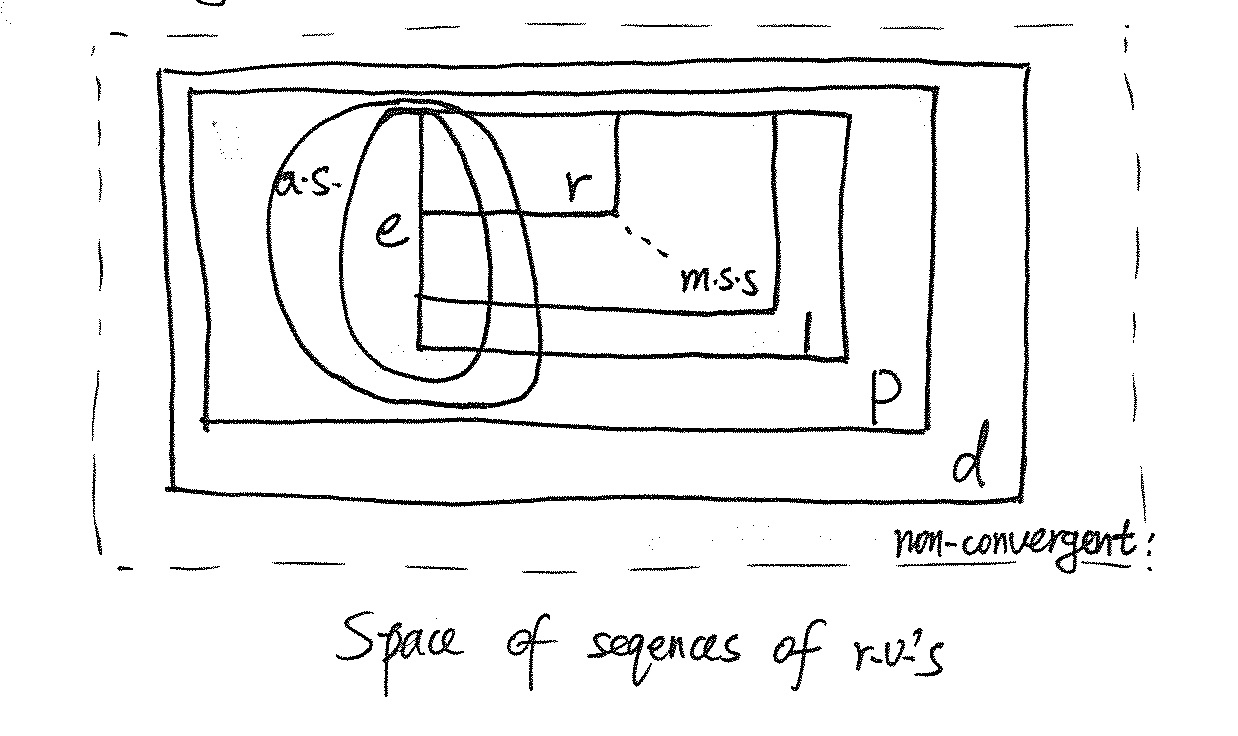Relations of convergence modes
If the limit is degenerate, i.e. a constant, then convergence in probability is equivalent to convergence of distribution functions.
(Proof)
Convergence in probability and convergence of expectation are distinct concepts.
Neither of them implies the other.
Convergence of expectation is defined as: $$\lim_{n\to\infty} \mathbb{E}[Z_n - Z] =0$$
Convergence of expectation is related to convergence in $L_1$, but much weaker. Still, it's not weaker than convergence in probability. Counterexamples typically have unbounded heavy tail. Consider sequence $Z_n$ which takes value n with probability $\frac{1}{n}$, and equals 0 otherwise. This sequence converges to degenerated r.v. 0 in probability, but converges to 1 in expectation.