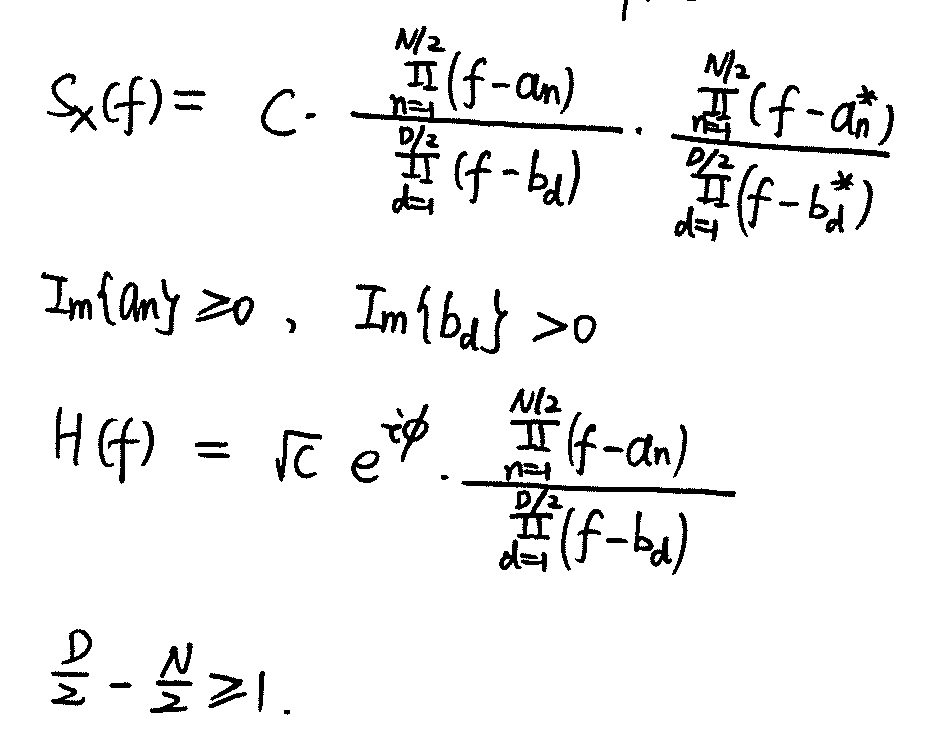Simulation
Realizable Systems (Chap 22.4)
Causality and spectral factorization (Chap 22.4)
Simulating a w.s.s. Random Sequence (Chap. 15.4)
- $\int_{-\frac{1}{2}}^{\frac{1}{2}} |\ln S_X{f}| \mathrm{d} f < \infty$
- $G(f) = \exp{\frac{a_0}{2} + \sum_{n=1}^{\infty} a_n z^{-n} }$, where $a_n = \int_{-\frac{1}{2}}^{\frac{1}{2}} \ln S_X{f} e^{i2\pi fn} \mathrm{d} f$, $z=e^{i2\pi f}$
- Causal iff $G_Z(z)$ analytic on and outside unit circle.
- $S_X(f)$ is real, then $S_X(z)$ zeros/poles are in conjugate reciprocal pairs; $S_X(f)$ is nonnegative, then $S_X(z)$ zeros/poles are on unit circle and have even order; $R_X(0) <\infty$, then there are no poles on unit circle
- on unit circle, $z^{-1} = z^{*}$
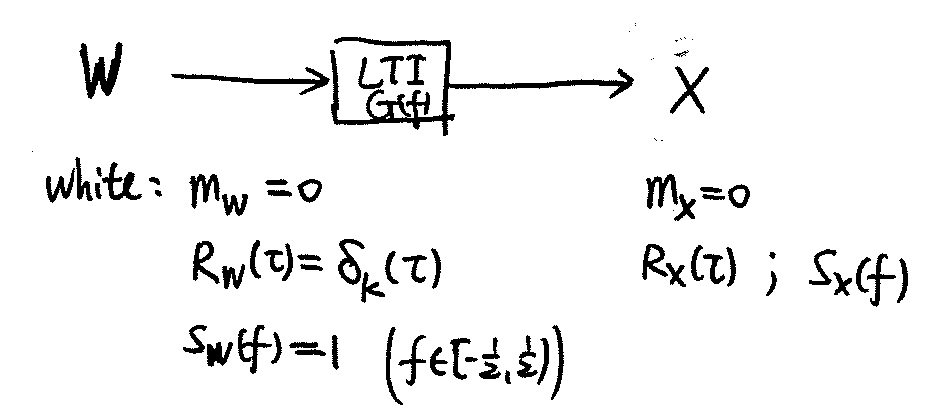
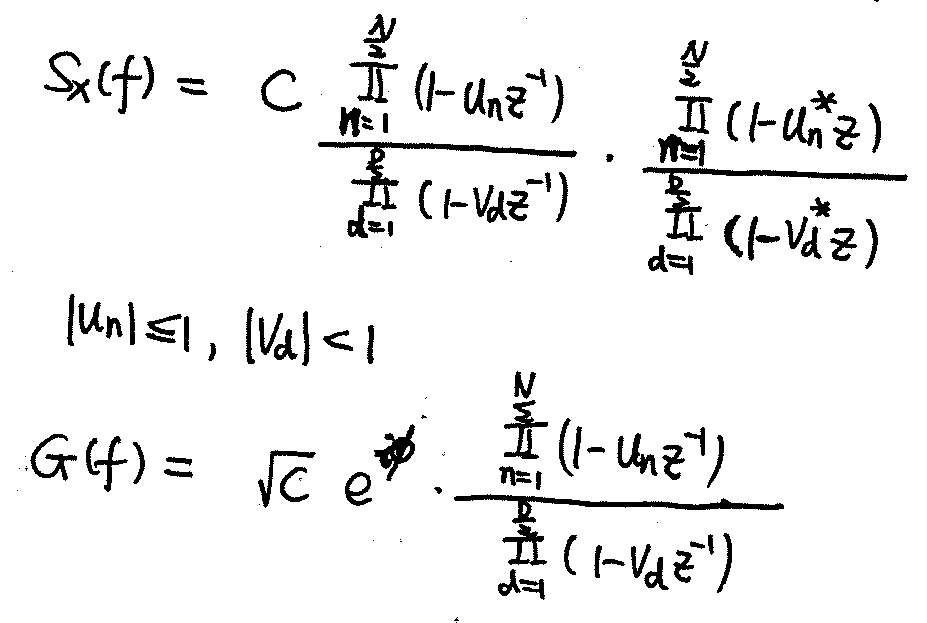
Simulating a w.s.s. Random Waveform
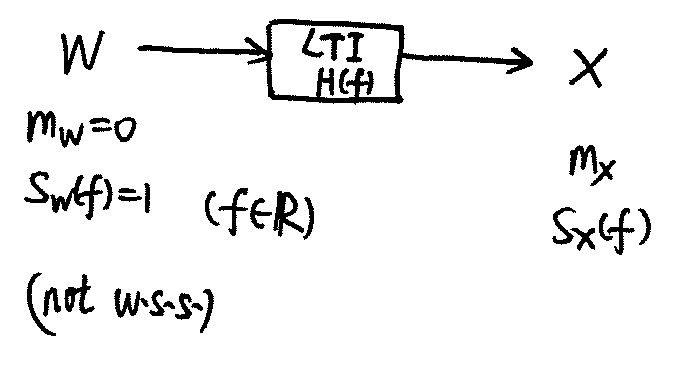
- $S_X(f)$ is real, then zeros/poles are in conjugate pairs; $S_X(f)$ is nonnegative, then $S_X(z)$ zeros/poles have even order; $R_X(0) <\infty$, then there are no real poles.
- Causal iff $H(f)$ analytic on and below real line.
- $X(u,t)$ being real implies poles/zeros of $S_X(f)$ are symmetric about the origin.