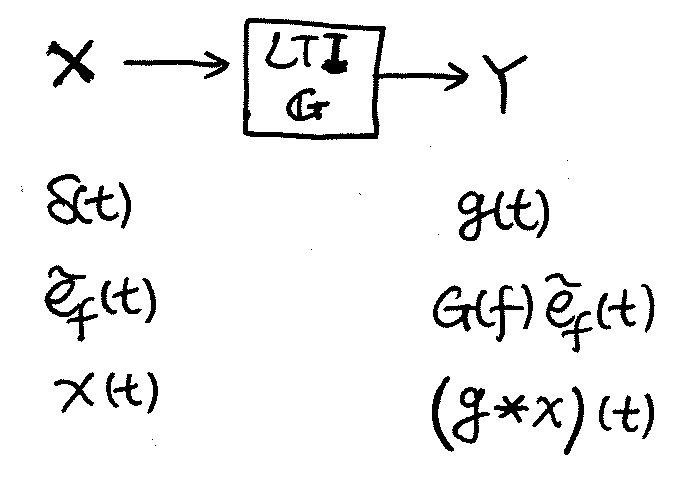
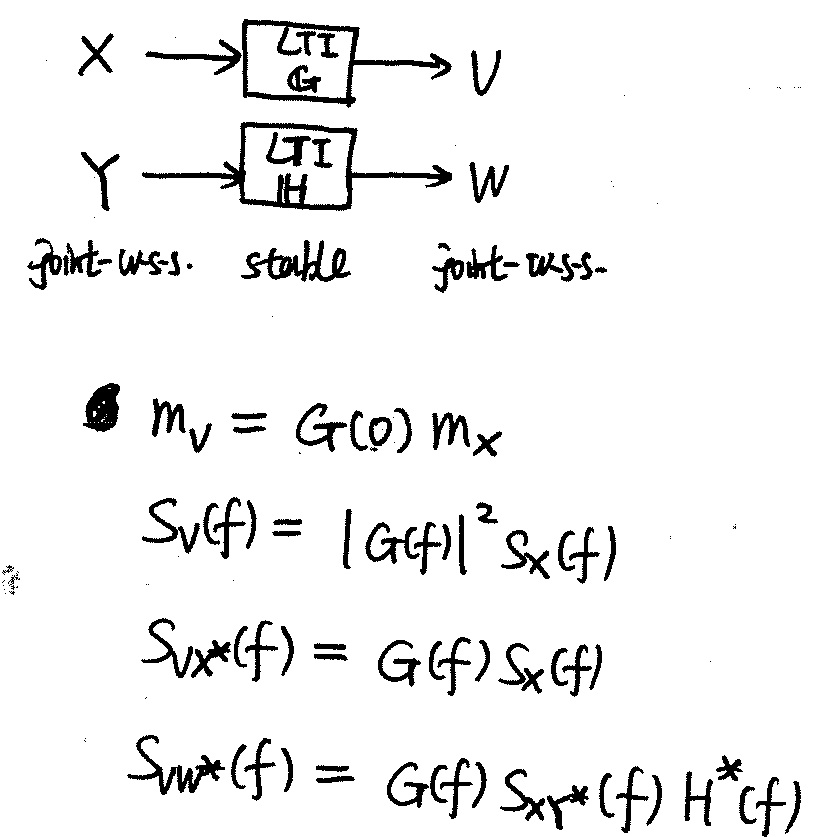System
Linear Time/Translation Invariant (LTI) Operators (Chap.
22.1)
- e-function: $\tilde{e}_f(t) = e^{i2\pi ft}$
- $G(f) = \mathcal{F}{ g(t) }$
- stable: bounded input produces bounded output
- Given $\mathbb{H}$ is LTI. Stable is equivalent to $h(t)$ absolutely integrable.
- Given $\mathbb{H}$ is LTI. Causal is equivalent to $h(t)=0, \forall t<0$.